Описание локальной контекстно-зависимой метрики

Существуют разные способы разбиения множества объектов на классы:

Привлечение экспертного знания. Оно может выражаться, например, в ограничениях, накладываемых на диапазоны изменений признаков объектов, или же в формулировании набора правил для разбиения объектов на классы (построение классификатора).
Разбиение на основе обучающей выборки, представленной экспертом (обучение с учителем).
Кластеризация.

Локальная метрика, основанная на классах эквивалентности, делит все объекты на две группы: входящие в один класс с текущим и не входящие в этот класс. Она может принимать только два значения. Если исследуемый объект попал в класс, то близкими (равными по метрике) ему могут считаться объекты этого же класса. Остальные - не равны. Такая метрика не полностью учитывает взаимоотношения между текущим объектом и окружающими (контекст), особенно когда объект попадает в область пересечения классов.

Формирование классов происходит до рассмотрения исследуемого объекта и естественно, не в его признаковом пространстве. На этапе предварительной обработки, когда объекты собирают в классы, признаковым пространством для класса будет пространство, общее для всех признаков этого класса. Далее, после того, как классы сформированы, естественно рассматривать их в общем для них признаковом пространстве (в транзитивном замыкании пространств всех объектов).

При рассмотрении исследуемого объекта он может быть отнесен сразу к нескольким классам. Такая ситуация может возникать, если у объекта часть признаков по отношению ко всем этим классам отсутствует. Это же может произойти из-за недостаточной или некачественной информации при обучении или при разделении на классы. На практике возникновение подобных ситуаций не является редкостью. Проиллюстрируем их на простом примере (рис. 7).

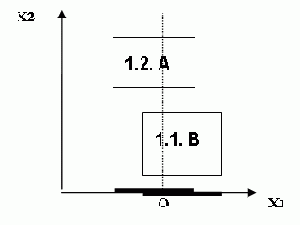
Рис. 7.Отнесение недостаточно описанного объекта к двум классам.

Два непересекающихся класса A и B описаны в пространстве признаков {X1, X2}. Объект исследования O представлен одним признаком X1, признак X2 у него отсутствует.

В этом пространстве признаков {X1} проекции классов пересекаются, и объект попадает в это пересечение.
Для более точной оценки нужно было бы добавить к контрольному объекту значение признака X2 (так же поступают и в медицине: если имеющихся показателей не хватает для дифференцирования заболеваний, только дополнительное исследование позволит сделать окончательный вывод), но на практике это не всегда возможно.
До сих пор считалось, что попадание объекта в область пересечения классов является препятствием для оценки объекта. Поскольку от этой ситуации избавиться не удается, ее надо постараться использовать. Для этого будем использовать аналоги - объекты соответствующих классов, попадающие в ту же область пересечения.
При рассмотрении объекта соответствующая ему точка сравнивается с расположением классов в проекции на пространство его признаков. Другие объекты, входящие в один класс с ним, считаются близкими к нему. Объекты могут также попадать в область пересечения классов. Все объекты можно разделить на группы (рис. 8), основываясь на сложности этого пересечения. Объекты, находящиеся в той же области пересечения, что и исследуемый объект, естественно считать более близкими к нему, чем те, которые находятся вместе с ним в каком-нибудь одном из классов, не входя в область пересечения. Этому можно найти простое объяснение: если считать, что введением классов мы разбили множество объектов на основные понятия, то с тем же набором признаков, что и текущий объект, они подобны ему по принадлежности к понятиям, обозначаемым классами.
Сравнив введенное понятие близости с тем, что говорилось ранее, нетрудно заметить, что предложенная метрика является локальной и контекстно-зависимой. Локальной, потому что привязана к рассматриваемому объекту, контекстно-зависимой - потому что зависит от его набора признаков. Приведем более строгое определение предлагаемой меры:
Расстояние от текущего объекта до другого равно разности количества классов, куда попал текущий объект, и количества классов из этого числа, в котором находится другой.
Это значит, в частности, что расстояние между текущим объектом и другим объектом, находящимся в той же области пересечении классов, равно нулю. На рис. 8 цифрами помечены области с соответствующим этим цифрам расстоянием от текущего объекта до объекта из этой области.
Предложенная мера не является метрикой в классическом понимании, а только имеет интерпретацию расстояния. Для нее не гарантируется выполнение правила симметричности, потому что она привязана к объекту, и, при переходе к другому объекту, будет рассматриваться уже в его пространстве признаков. По этой же причине не гарантируется выполнение правила треугольника. Однако она позволяет учитывать контекст взаимоотношений объекта с окружающими, особенно в непосредственной близости от него.

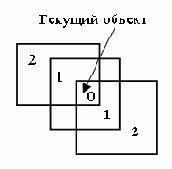
Рис. 8. Степени близости объектов.

Содержание раздела